Câu chuyện
Hơn 10 năm trước, năm 2013, khi mình ôn luyện để đi thi tin học trẻ quốc gia, thầy đã cho mình làm thử đề thi của những năm trước, trong đó có một bài toán lăn xúc xắc mà cả thầy và trò đều phải bó tay. Mình nhớ, ngay cả bạn giỏi nhất trong đội tuyển cũng đã phải rất trăn trở với bài này. Mình không biết cuối cùng bạn ấy có giải ra không, nhưng về phần mình thì mình đã phải đầu hàng bỏ cuộc. Kể từ đó, cứ khoảng vài năm mình lại nhìn lại bài toán này, nhưng cũng không giải được. Mình quên nó hẳn đi khi mình vào đại học. Năm nay mình đã đào lại bài toán xưa với hi vọng là mình đã thông minh hơn hồi trước để giải nó. Và cuối cùng là mình đã giải được!
Mời bạn đọc đề bài đầy đủ tại đây.
Tóm tắt bài toán
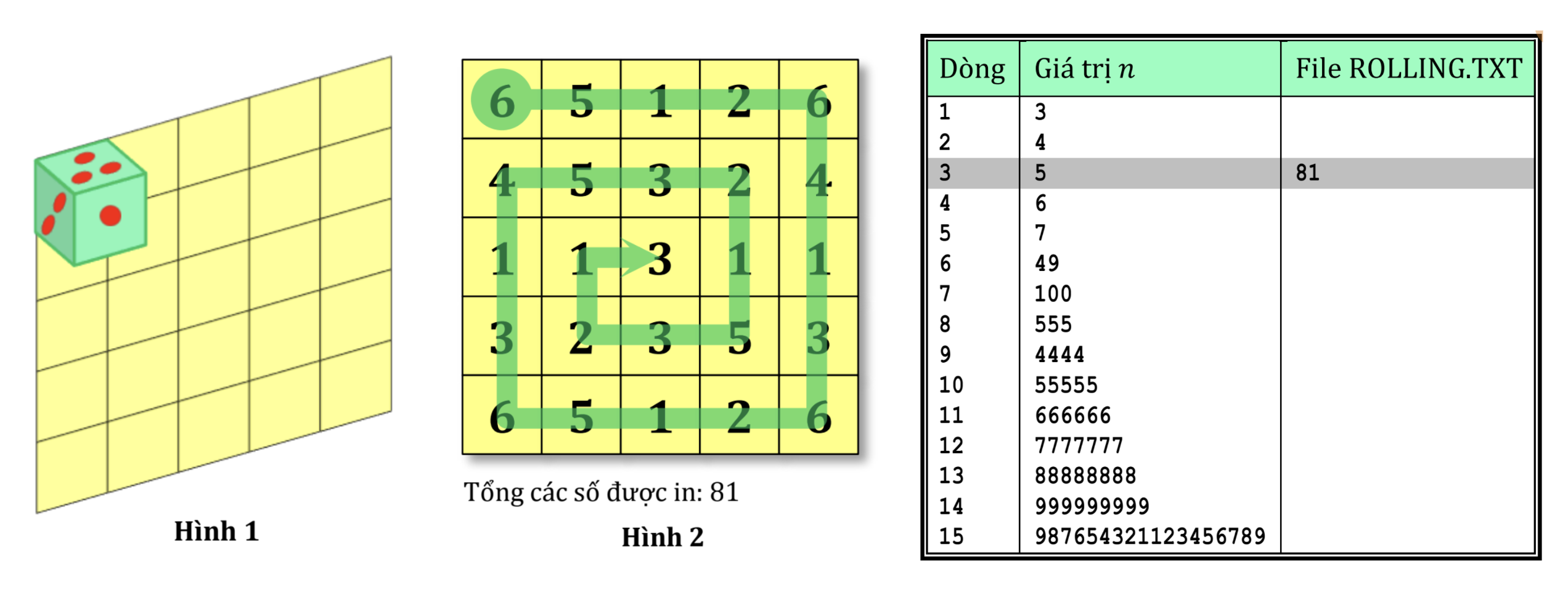
Cho một bàn cờ kích thước ô vuông và một con xúc xắc nằm ở ô góc trên bên trái. Lần lượt lăn xúc xắc theo hình trôn ốc theo chiều kim đồng hồ cho đến khi tất cả các ô được bao phủ. Tại mỗi ô, xúc xắc để lại giá trị đúng bằng giá trị mặt dưới của xúc xắc tại thời điểm nó tới. Tính tổng giá trị của tất cả các ô trên bàn cờ.
Một vài ý tưởng
Cách giải
Ý tưởng đơn giản nhất là mô phỏng lại toàn bộ quá trình trên để tạo ra một mảng hai chiều chứa giá trị của tất cả các ô trên bàn cờ. Vấn đề duy nhất của cách này đó là làm sao để di chuyển hai chỉ số và (“c” viết tắt của “current”). Ta thấy rằng xúc xắc luôn bắt đầu bằng việc lăn sang phải, đến giới hạn thì lăn xuống, đến giới hạn nữa thì lăn sang trái, đến giới hạn nữa thì lăn lên trên, rồi lặp lại: phải, xuống, trái, lên. Ta đánh ký hiệu:
- Chiều “0” là chiều đi sang phải, khi đó chỉ số phải được giữ nguyên, còn thì cộng 1.
- Chiều “1” là chiều xuống dưới, khi đó được cộng 1, còn giữ nguyên.
- Chiều “2” là chiều qua trái, giữ nguyên, bị trừ 1.
- Chiều “3” là chiều lên trên, bị trừ 1, giữ nguyên.
Xúc xắc được xem là đã “lăn đến giới hạn” nếu ô tiếp theo trên chiều đi của nó đã được đặt chân đến trước đó hoặc nằm ngoài biên giới của bàn cờ.
Điều đầu tiên khi đặt chân đến mỗi ô là ghi nhận giá trị của ô đó, sau đó “thử” ô tiếp theo xem có hợp lệ hay không, nếu hợp lệ thì tiếp tục đi chiều đó, nếu không thì phải “tăng” chiều lên 1 đơn vị rồi modulo 4 (chiều 0 → 1, 1 → 2, 2 → 3, 3 → 0). Nếu đi theo chiều mới này vẫn không hợp lệ thì coi như tất cả các ô đã được điền giá trị.
Khi đã xác định được chiều đi hợp lệ, gọi các hàm
rollRight, rollLeft, v.v. tương ứng. Các hàm này chỉ đơn thuần đảo giá trị của các biến d, r, l, f, b, u (viết tắt của “downside”, “right side”, “left side”, “front side”, “back side”, “upside”). Mình sẽ không mô tả thêm cách đảo giá trị cụ thể như thế nào để tránh làm loãng bài viết.vector<vector<int>> generate(int n) {
vector<vector<int>> ans(n, vector<int>(n, 0));
int ci = 0, cj = 0;
int di = 0, dj = 1;
int direction = 0;
while (true) {
ans[ci][cj] = d;
if (!(ci + di >= 0 && ci + di < n && cj + dj >= 0 && cj + dj < n && ans[ci + di][cj + dj] == 0)) {
direction += 1; direction %= 4;
if (direction == 0) {
di = 0; dj = 1;
} else if (direction == 1) {
di = 1; dj = 0;
} else if (direction == 2) {
di = 0; dj = -1;
} else {
di = -1; dj = 0;
}
}
if (!(ci + di >= 0 && ci + di < n && cj + dj >= 0 && cj + dj < n && ans[ci + di][cj + dj] == 0)) {
break;
}
ci += di;
cj += dj;
if (direction == 0) {
rollRight();
} else if (direction == 1) {
rollDown();
} else if (direction == 2) {
rollLeft();
} else {
rollUp();
}
}
int sum = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
sum += ans[i][j];
printf("%d ", ans[i][j]);
}
cout << endl;
}
cout << sum << endl;
return ans;
}Liệu có cách làm nào nhanh hơn không? Có.
Cách giải
Định nghĩa 1: Trạng thái của một xúc xắc bao gồm giá trị của 6 mặt: trên, dưới, trái, phải, trước, sau.
Ta nhận thấy có ba tính chất trong bài toán này:
Tính chất 1: Lăn xúc xắc 4 lần trên cùng một chiều thì xúc xắc trở về trạng thái ban đầu.
Tính chất 2: Tổng hai mặt đối diện của xúc xắc luôn bằng 7.
Tính chất 3: Trạng thái xúc xắc sau khi lăn lần trên cùng một chiều giống hệt như trạng thái sau khi lăn lần trên cùng chiều ấy.
Từ đó suy ra, ta có thể tính tổng của một đoạn thẳng độ dài ô bằng cách lấy cộng với tổng giá trị khi lăn xúc xắc đi ô. Như vậy, thay vì ngồi lăn tới ô thì giờ bạn chỉ cần lăn ô. Với phép rút gọn này, bạn có thể tính tổng các ô trên chu vi bàn cờ chỉ trong . Nhược điểm của cách làm này đó là bạn vẫn phải lưu trữ trạng thái của xúc xắc và vẫn phải tiếp tục mô phỏng việc lăn xúc xắc. Một khi bạn hoàn thành vành chu vi của bàn cờ và tiến vào vành tiếp theo, trạng thái xúc xắc đã hoàn toàn khác. Có vành hình vuông trên bàn cờ, bạn phải lặp lại phép tính này cho mỗi vành, do đó độ phức tạp của thuật toán này là .
Hồi mình còn nhỏ, mình chỉ đạt đến bước này và không tìm cách tối ưu nó thêm được nữa. Cho đến một ngày mình đã đi làm và giải toán chỉ còn là niềm vui, mình nhận ra một sự thật quá đỗi hiển nhiên.
Cách giải
Tính chất 4: Xúc xắc có tổng cộng đúng 24 trạng thái: chọn một trong 6 mặt dưới, rồi chọn một trong 4 mặt xung quanh làm mặt trước; .
Khi đủ lớn, cụ thể là đến mức để , thì chắc chắn sẽ đến một vành nào đó mà trạng thái ban đầu của xúc xắc được lặp lại (nguyên lý Dirichlet). Khi mô phỏng thử vài trường hợp, mình nhận ra rằng nếu là chẵn thì cứ lăn hết 6 vành xúc xắc sẽ lặp lại trạng thái ban đầu. Nếu là lẻ thì chu kỳ đó là 3.
Trạng thái xúc xắc ở ô đầu tiên của mỗi vành khi chẵn:
| D | U | R | L | F | B | |
|---|---|---|---|---|---|---|
| Vành 1 | 6 | 5 | 1 | 2 | 4 | 3 |
| Vành 2 | 4 | 6 | 3 | 1 | 5 | 2 |
| Vành 3 | 5 | 3 | 2 | 4 | 1 | 6 |
| Vành 4 | 1 | 5 | 6 | 2 | 3 | 4 |
| Vành 5 | 3 | 6 | 4 | 1 | 2 | 5 |
| Vành 6 | 2 | 3 | 5 | 4 | 1 | 6 |
| Vành 7 (như vành 1) | 6 | 5 | 1 | 2 | 4 | 3 |
Khi lẻ:
| D | U | R | L | F | B | |
|---|---|---|---|---|---|---|
| Vành 1 | 6 | 5 | 1 | 2 | 4 | 3 |
| Vành 2 | 5 | 3 | 2 | 4 | 1 | 6 |
| Vành 3 | 3 | 6 | 4 | 1 | 2 | 5 |
| Vành 4 (như vành 1) | 6 | 5 | 1 | 2 | 4 | 3 |
| Vành 5 (như vành 2) | 5 | 3 | 2 | 4 | 1 | 6 |
| Vành 6 (như vành 3) | 3 | 6 | 4 | 1 | 2 | 5 |
| Vành 7 (như vành 1) | 6 | 5 | 1 | 2 | 4 | 3 |
Để tiện tính toán, bạn có thể xem như khi lẻ chu kỳ cũng là 6, vì 6 chia hết cho 3.
Định nghĩa 2: Hai vành được gọi là đồng dạng nếu trạng thái xúc xắc tại điểm bắt đầu của hai vành là như nhau. Ví dụ, khi chẵn, vành 1, 7, 13, 19, v.v. là đồng dạng với nhau.
Gọi là tổng của một vành cạnh , còn là tổ hợp các mặt của xúc xắc tạo nên trạng thái của xúc xắc lúc đó. Gọi là tổng của của vành cạnh và tất cả các vành đồng dạng bên trong nó, ta có:
Khi đó, ta chỉ cần mô phỏng việc lăn cho 6 vành, và tổng của toàn bàn cờ sẽ bằng:
Trong đó, là trạng thái xúc xắc tại vành thứ (Vành 1 là vành chu vi).
Lưu ý, với tính chất 3 kể trên, bạn hoàn toàn có thể sinh ra các trạng thái chỉ trong vòng .
Bài toán tìm hàm có thể được diễn đạt như sau:
Cho một xúc xắc ở ô góc trên bên trái của bàn cờ kích thước . Xúc xắc có mặt dưới là , trên , trái , phải , trước , sau . Tính tổng các giá trị trên chu vi của bàn cờ sau khi lăn xúc xắc như mô tả ở đề bài.
(Ta chỉ phát biểu bài toán chứ không lập công thức hàm , ta sẽ tính thẳng công thức hàm )
Để làm được điều này, bạn cần phải biết tần số xuất hiện của , , , , , . Tần số này cũng phụ thuộc vào số dư khi chia cho 4. Cụ thể:
| nếu nếu | ||||
(Bạn đọc tự chứng minh)
Ta thấy, công thức tần số luôn có dạng (tạm thời đừng để ý đến ngoại lệ duy nhất trong bảng)
Ta biết rằng cứ lăn hết 6 vành thì chắc chắn trạng thái xúc xắc trở lại ban đầu. Lúc vào đến vành thứ 7, kích thước còn lại của bàn cờ chỉ là . Vậy, nếu ở vành thứ nhất, tần số của một giá trị là thì:
- Ở vành thứ 7, tần số của giá trị đó là
- Ở vành thứ 13, tần số của giá trị đó là
- Ở vành thứ , tần số của giá trị đó là . Có thể thấy, , suy ra . Mà là số không âm, nên .
Đặt . Vậy, tổng tần số của giá trị đó ở vành 1, 7, …, là:
Trở lại hàm nói trên, lúc này để tính , trước hết ta tính , sau đó, với mỗi giá trị từ 1 đến 6:
- Tìm xem nằm ở mặt nào trên xúc xắc ở ô ban đầu.
- Tuỳ vào việc là mặt trên, dưới, trái, phải, trước, sau, hãy tra bảng tần số để tìm giá trị và .
- Tính .
Tổng tất cả các tích tính được ở trên sẽ bằng tổng .
Sau đó, bạn mô phỏng quá trình lăn xúc xắc quanh 1 vành bàn cờ (có thể lăn rút gọn như đã đề cập ở trên), bắt đầu tính tiếp , v.v. cho đến .
Kết quả bài toán sẽ là:
Có một ngoại lệ duy nhất khi tính đó là nếu thì ta phải cộng kết quả với mặt dưới của . Lý do là khi thì công thức trong bảng cho ra kết quả là 0 trong khi nó phải là .
Source code C++ cho lời giải :
#include <bits/stdc++.h>
using namespace std;
int d = 6, r = 5, u = 1, l = 2, f = 4, b = 3;
void setDice(int _d, int _r, int _u, int _l, int _f, int _b) {
d = _d;
r = _r;
u = _u;
l = _l;
f = _f;
b = _b;
}
void resetDice() {
setDice(6, 5, 1, 2, 4, 3);
}
void rollRight() {
int _r = u, _u = l, _l = d, _d = r;
setDice(_d, _r, _u, _l, f, b);
}
void rollDown() {
int _f = u, _u = b, _b = d, _d = f;
setDice(_d, r, _u, l, _f, _b);
}
void rollLeft() {
int _l = u, _u = r, _r = d, _d = l;
setDice(_d, _r, _u, _l, f, b);
}
void rollUp() {
int _f = d, _d = b, _b = u, _u = f;
setDice(_d, r, _u, l, _f, _b);
}
pair<int, int> formulae[6][4] = {
{{3, -1}, {4, 0}, {3, 2}, {4, 2}},
{{3, 0}, {4, 0}, {3, 0}, {4, 2}},
{{3, 0}, {2, 0}, {3, 1}, {2, 2}},
{{3, -2}, {2, 0}, {3, 0}, {2, 0}},
{{2, 0}, {2, 0}, {2, 1}, {2, 2}},
{{2, -1}, {2, 0}, {2, 0}, {2, 0}},
};
int calc2(int n) {
resetDice();
int sum = 0;
for (int i = 0; i < 12 && n - i > 0; i += 2) {
int faces[6] = {d,u,r,l,f,b};
int _n = n - i;
int k = (_n - 1) / 12;
for (int j = 0; j < 6; j++) {
int v = faces[j], p = formulae[j][_n % 4].first, q = formulae[j][_n % 4].second;
sum += v * p * (_n / 4) * (k + 1) - 3 * p * v * (k * (k + 1) / 2) + v * q * (k + 1);
}
for (int i = 0; i < (_n - 1) % 4; i++) {
rollRight();
}
for (int i = 0; i < (_n - 1) % 4; i++) {
rollDown();
}
for (int i = 0; i < (_n - 1) % 4; i++) {
rollLeft();
}
for (int i = 0; i < (_n - 2) % 4; i++) {
rollUp();
}
rollRight();
}
if (n % 2 == 1) {
int x = (n + 1) / 2;
if (x % 3 == 0) {
sum += 3;
} else if (x % 3 == 1) {
sum += 6;
} else {
sum += 5;
}
}
cout << sum << endl;
return sum;
}
int main() {
int n = 7;
calc2(n);
return 0;
}Kết luận và chém gió
Rõ ràng ta đã tối ưu hoá độ phức tạp thuật toán hết mức có thể, chỉ còn . Nhưng đề bài gốc của kỳ thi năm ấy cho lên đến gần 1 tỷ tỷ, chính xác là , và yêu cầu phải tính ra tổng tuyệt đối. Thông thường những bài toán yêu cầu phép tính với số lớn như thế này, họ sẽ cho phép bạn đưa ra kết quả sau khi đã modulo cho một số nguyên tố lớn chấp nhận được như . Ở đây, bạn lại phải tính ra số chính xác.
Số lớn như thế này, một là bạn dùng thư viện
BigInteger của Java, hai là bạn tự viết hàm cộng trừ nhân chia số lớn, ba là bạn tính lập trình bằng Python thì nó tự xử lý số lớn cho bạn. Mình quen dùng C++ nên mình đã copy code trên và transpile nó sang Python rồi đưa số lớn vào.Bài này không những hóc búa về mặt tối ưu thuật toán mà còn tréo ngoe ở cái test case cuối cùng. Thời đó, mình chỉ được học ngôn ngữ Pascal, nên mình cũng không nhớ hoặc không chú ý là trên máy tính phòng thi có lập trình Java được không (cho dù nếu được thì cũng chỉ có lợi cho bạn nào biết code Java). Mình nghĩ là đại đa số học sinh thời ấy dùng Pascal (đối với học sinh cấp 2) và C++ (cấp 3) cho những kỳ thi như thế này. Mình tin rằng test case này cho là để khống chế thí sinh khỏi điểm tuyệt đối.
Cá nhân mình thấy bài này thực sự quá khó để học sinh cấp hai có thể giải tới . Mình cũng không đề cao việc ban tổ chức “giấu” lời giải, để thầy trò mình năm xưa vất vả mấy ngày liền mà vẫn không tìm ra đáp án. ==”
Mời bạn xem bảng đáp án cho 15 test của đề:
| Kết quả | |
|---|---|
| 3 | 37 |
| 4 | 62 |
| 5 | 81 |
| 6 | 121 |
| 7 | 180 |
| 49 | 8406 |
| 100 | 35006 |
| 555 | 1078093 |
| 4444 | 69121982 |
| 55555 | 10802253096 |
| 666666 | 1555552444441 |
| 7777777 | 211728352716054 |
| 88888888 | 27654320434567910 |
| 999999999 | 3499999993000000009 |
| 987654321123456789 | 3414113703118427061341792408625666823 |